Linear Regression / 선형 회귀

Definition

Data

세상 모든 데이터를 independent variable x와 Dependent variable y로 구분해보자.

x는 관찰 값(observations)이고 y는 관찰 값에 대응하는 결과 값(labels)이다.

 

우리의 목적은 알려진 x, y로 학습된 모델이 새로운 x를 입력 받았을 때 그에 대응하는 y를 더 정확히 산출하게 하는 것이다.

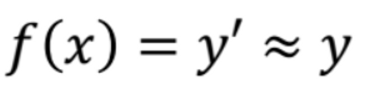
Linear regression

위의 목적을 해결하기 위한 비교적 쉬운 방법 중 하나는 linear regression이다.

그것은 x와 y에 선형적인 관계가 있다고 정의하고, ( f(x) = y ) → ( ax + b = y )로 정의한다음 그 관계를 제일 잘 나타내는 파라미터 a를 찾아보는 것이다. a는 x에 어떤 계산을 해야 y가 나오는지에 대한 변수라고 볼 수 있다. 즉, a를 찾는 것은 x와 y의 관계를 찾는 것과 같다.

 

 

Parameter and Cost function

파라미터 a를 잘 찾으면 입력값 x에 대해 모델이 뱉는 y는 실제 데이터와 비슷해질 것이고 직선은 다음과 같아질 것이다.

파라미터 a를 잘 찾는 방법은 같은 x에 대해 원래 존재하던 y값과 우리 모델이 뱉어낸 y’값의 차이를 줄이는 것이다.

저 격차를 줄이는 방향으로 파라미터를 조절하는 것은 직선의 기울기를 조정하는 것과 같다.

 

저 격차를 cost(loss)라고 부르고, 우리는 cost가 0이 되는 것을 목표로 삼아야 한다.

그러려면 전체 x에 대해 모델이 뱉어낸 y’과 실제 y 사이의 cost를 구하는 함수를 만들고, 그 함수의 결과가 최소 값이 나오게 하는 방향으로 a를 설정해야 한다. (하지만 cost 함수의 결과 값이 0 되는 것은 현실적으로 어려운 일이다.)

 

다시 한번 말하자면, cost 함수는 전체 데이터의 cost를 고려한 것이다.

때문에 전체 cost의 최소 값을 계산하는 것에 대한 여러 방법론이 존재한다.

 

Linear Regression은 비교적 간단해서 다양한 방법을 적용할 수 있지만 그 중 가장 쉬운 방법들을 살펴보자

• MAE (Mean Absolute Error) - 에러의 절대 값을 최소화 하자
• MSE (Mean Squared Error) - 에러의 제곱의 평균을 최소화 하자

 

위와 같은 Cost Fucntion을 C(x)로 정의한다면, C(x)의 입력 값은 무엇이 될까?

모델의 예측 값 y’과 실제 y값. 그리고 모델의 예측 값 y’를 구하기 위한 모델 자체가 입력이 될 것이다.

 

 

그 모델은 파라미터 a와 관찰 값 x를 입력으로 받는다.

Cost Fuction으로 MSE를 선택하여 식을 만들어 보면 다음과 같다.

 

y’은 모델의 아웃풋이므로 x와 a(w)로 정의된다.

 

 

최종적으로, 우리는 a의 값을 바꿔줌으로써 모델이 뱉어내는 y’의 값을 y와 같아지게 해야 한다.

 

꽤 간단해 보인다. 만약 a를 무작위로 설정해 위와 같은 그래프가 나왔고, x가 4일 때 C(x)의 값이 0이 되면서 운이 좋게도 최적의 결과를 찾을 수도 있다. 이렇게 최적의 결과를 찾는 것을 Optimazation이라고 한다.

 

 

하지만 파라미터 하나로 x와 y의 관계를 계산하는, 정의하는 것은

사람이 봐도 무엇인지 알 수 없는 갈색 선이 그려져 있는 그림을 모델에게 줬을 때 그것이 동물의 갈색 털을 의미하는 것이며, 그 동물은 호랑이임을 판별하는 것을 기대하는 것과 같다.

 

그럼 파라미터를 한 개 더 늘려보자.

 

c(x)의 값을 결정 짓는 인자가 2개이므로 결과는 3차원이 된다. parameter space는 우리가 찾을 수 있는 파라미터들의 가능한 조합을 모아놓은 것이다.

 

모델을 더 정교하게 하기 위해 파라미터를 더 늘린다면?

여기서 파라미터를 하나만 더 늘려도 parameter space가 4차원이 되면서 사람이 직관적으로 인지하기 힘들어지는데, 보통 파라미터의 갯수는 엄청나게 큰 숫자이다.

 

GPT-3는 1700억개의 파라미터를 가지고 있고, 그 파라미터의 조합은 무한대이다. GPT-3의 최적 파라미터를 찍어서 찾을 확률 또한 무한대이다.

 

이렇게 더 정확한 모델을 위해 파라미터를 찾는 것을 Optimazation, Training이라고 한다.

 

 

Traning Algorithms

Parameter Search를 위한 Traning function 또한 Cost function과 마찬가지로 여러 방법이 존재한다. 물론 이 두 알고리즘도 아직 계속해서 발전해나가는 과정에 있다.

 

Training function의 목적은 파라미터들의 값을 바꿔 Cost Fuction의 최소 값을 찾는 것임을 다시 한번 상기하고 알고리즘을 살펴보자.

 

 

Gradient descent

우리가 첫 번째로 살펴볼 알고리즘은 것은 가장 쉽고 직관적인 이해를 빠르게 얻을 수 있는 Gradient Descent (경사 하강)이다.

 

경사 하강이란, Cost Function의1차 미분(First-order method), 즉 Cost Function의 기울기가 점점 낮아지는 방향으로 최적의 값을 찾는 방법이다.

위 그림에서 보다시피, Traning algorithm은 기본적으로 최적의 값이 나올 때 까지 반복적인 작업을 수행하는 것이다.

w는 특정 x와 파라미터 a1의 값이 들어가 있는 모델이다.

Cost Function의 값이 최적이 아닐 때 현재 기울기가 양수라면 기울기를 줄이고, 음수라면 더하는 방향으로 0이 되는 지점에 가까이 갈 수 있다.

1. CostFuntion을 미분하여 그 점에서의{ w(a,x) } 기울기의 부호를 본다.
2. 그것을 빼거나 더함으로써 더 낮은 기울기로 갈 수 있다.
3. 더 낮은 기울기로 향한 다는 것은 w(a, x) 에서 최적의 a를 찾는 것과 같다.

 

Optimal gradient

이렇게 찾은 a는 고정된 x에 대한 모델의 Cost Function에서의 최적의 파라미터이다.

이는 X(observation)하나에 대한 최적 값이라고 할 수 있다.

방대한 데이터를 학습시켜야 되는 입장에서 Cost Function 또한 데이터의 숫자만큼 늘어날 수 밖에 없다.

 

최적의 기울기란 모든 데이터에 대한 평균의 기울기이다. 즉 평균 에러를 최소화 하는 것과 같다. 각 데이터의 에러를 최소화하는 것이 아니다.

 

 

Learning Rate

경사 하강법을 반복하면서 기울기를 찾는데, 한 점에서의 기울기가 너무 크면 다음에 위치할 점의 반경 또한 커진다.

이는 학습에서 제일 중요한 요인 중 하나이다.

 

때문에 우리는 Learning Rate라는 변수를 기울기에 곱해줌으로써 전체 Traning의 속도를 조절할 수 있다.

일반적으로, 최적의 Learning rate를 구하는 계산 방법은 없다. 찍어야 한다.

 

데이터마다 특성이 너무나 다양하고 Cost 또한 달라지기 때문에 매 학습마다 찍어서 조절하는 수밖에 없다.

정확도를 위해 Learning rate를 너무 작게 설정하면 필요 이상으로 학습이 더뎌지고, 빠른 학습을 위해 너무 크게 하면 세 번째 그림과 같이 overshooting이 발생할 수도 있다.

 

 

지금까지의 설명은 Cost Function이 Convex하기 때문에 이해하기 쉽다.

(convex는 2차 함수 처럼 휘어지는 구간이 하나인 것을 말함, 밥그릇 모양)

하지만 Cost Fuction이 MSE나 MAE처럼 2차 함수가 아닌 더 복잡하고 non-convex한 함수라면?

 

기울기가 0이지만 Cost Function의 값이 최소가 아닌 값이 여러 곳에 존재할 수 있다.

Parameter Space가 다차원인 것 또한 경사 하강법을 더 복잡하게 만드는 또다른 이유이다.

 

 

Closed Form

Closed Form은 애초에 cost(W)식을 미분하여 0인 점을 찾는 알고리즘으로 역행렬이 존재한다면 closed-form으로 해를 찾는 것이 가능하므로 학습 과정 없이 한번에 최적 파라미터를 구하는 방법이다.

 

 

하지만 대부분의 non-linear regression문제는 closed form solution이 존재하지 않고, losed form solution이 존재해도 수많은 parameter가 있을때는 GD로 해결하는 것이 계산적으로도 더 효율적이다.

데이터가 클수록 역행렬을 구하는 것이 복잡할 뿐더러 없는 경우도 많다.